Statistical Hypothesis Skepticism: Implications for Credit Risk

Financial risk managers continue to rely heavily on statistical hypothesis testing in modeling and statistical analysis, even though a group of scientists are now arguing that these tests have lost their relevance.

Recently, in fact, some scientists have gone so far as to declare probability value (P-value), an important statistical measurement tool, obsolete, advocating for its elimination. For instance, the editors of the Journal of Basic and Applied Social Psychology (JBASP) have described the null hypothesis significance testing procedure (NHSTP) as “invalid,” while mandating their authors to omit “all vestiges of the NHSTP” – including P-values, F-values and T-tests.

But are these arguments logical, and just how much weight do they hold in the financial risk management community?

Marco Folpmers

P-values, after all, are still used to determine if the probability of default (PD) is underestimated with the Jeffreys test. They’re also useful in figuring out whether  a coefficient should be added to an early warning system, and they can help assess whether the SICR criteria for IFRS 9 are effectively implemented. All these examples demonstrate the importance of hypothesis testing in credit risk analysis, much like in biomedical research.

Despite all this, NHSTP continues to face scientific criticism, and there remains an ongoing debate about the role of hypothesis testing and P-values in credit risk modelling.

So, who’s right and who’s wrong? Are the critiques of NHSTP by scientists valid or do these types of tests remain central to credit risk modeling? Perhaps the answer somewhere in between.

Let’s now explore answers to these questions, concentrating on one specific criticism: the bias associated with repeated hypothesis testing.

Repeated Hypothesis Testing

Consider building a causal model where a dependent variable is linked to a set of independent variables. Typically, if a variable shows significance with a P-value below 5%, it is retained. In credit risk modeling, P-values indicate the likelihood that observed dependencies are due to chance. A small P-value (under the 5% threshold) suggests a genuine relationship, rather than a random occurrence.

However, if you have a large set of independent variables or repeatedly test new drivers for significance, you risk committing a Type 1 error – one in which the null hypothesis is erroneously rejected (false positive). Repeated testing increases the likelihood of identifying a significant coefficient for a driver that does not actually influence the dependent variable. This results in falsely rejecting the null hypothesis.

The reasoning for such errors is straightforward: if we test at the 5% significance level, the chance of falsely rejecting the null hypothesis – and thereby accepting a false positive variable into the model – is 5%. However, if a non-significant coefficient is dismissed and a new driver is tested, the combined probability of erroneously rejecting the null hypothesis rises to 9.75%. Over six separate tests, the probability of falsely rejecting the null hypothesis increases to more than 25%.

In general, the formula for this so-called Family-Wise Error Rate is: 𝐹𝑊𝐸𝑅=1−(1−𝛼)𝑛. The FWER is a useful concept to illustrate how easy it is to get a spurious significant result if you perform enough tests. Figure 1 illustrates this formula for up to 20 tests.

Figure 1: Family Wise Error Rate

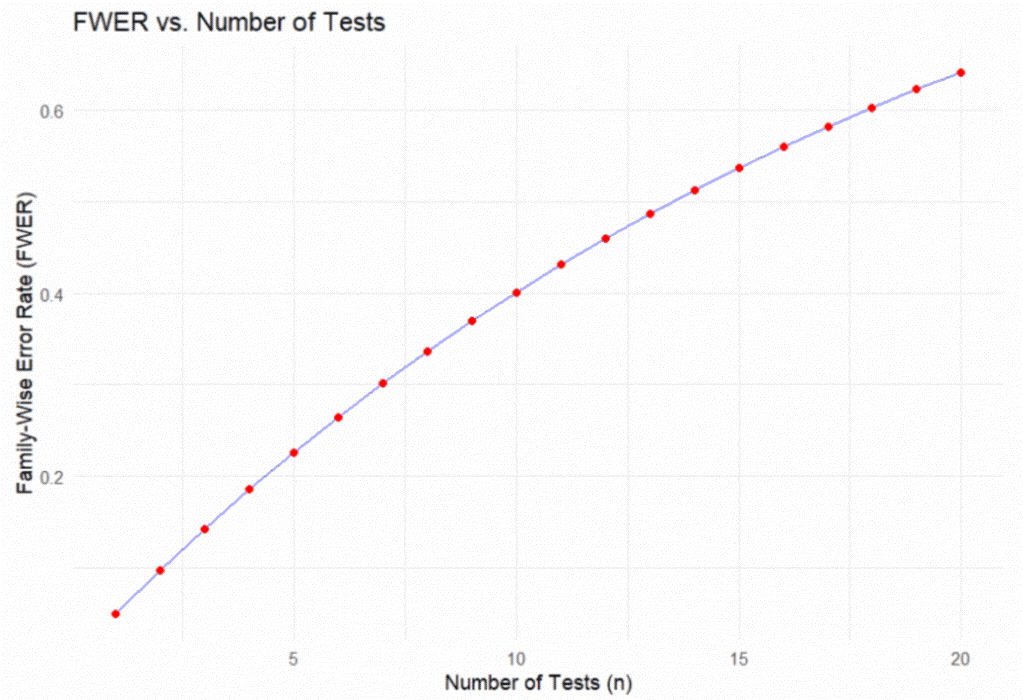
For financial risk managers, understanding the FWER is critical. It helps prevent the erroneous inclusion of a driver in a dependency model, where there is no relationship with PD, LGD or any other dependent risk parameter. Figure 1 demonstrates how the probability of making such an error increases rapidly with the number of tests conducted.

Very Small and Very Large Data Sets: The Same Mistake

The challenge with hypothesis testing intensifies with small data sets, where slight changes can significantly alter test statistics and P-values, often pushing them beyond the 5% cutoff. This makes decision-making based on these results seem arbitrary.

It's therefore understandable why editors of certain psychological journals are critical of hypothesis testing, even going so far as to ban articles focused on this issue or require them to be sanitized from all vestiges of statistical hypothesis testing. But does this imply that financial risk managers should also abandon traditional tests used for model development and validation?

Remember, repeated testing is common in credit risk modeling. Indeed, whenever new data sets are available, model builders test different drivers to enhance the model's discriminatory power.

Machine-learning (ML) models, moreover, face a related issue. These methodologies often handle extremely large data sets, with hundreds of potential drivers. Even without repeated testing, it's easy to mistakenly include an unrelated driver in the ML model, if its test statistic exceeds the confidence threshold.

P-value Benefits: Capturing Both Signal and Noise

To properly understand P-values, it's important to recognize that they provide "weight of evidence" for the null hypothesis in the form of a signal-to-noise ratio. For instance, the combination of the t-statistic and the P-value in a credit risk model considers the risk driver’s variation and reflects how far the coefficient is from zero. A larger difference and/or a smaller variation make it easier to reject the null hypothesis, suggesting that the driver significantly impacts the risk parameter.

There’s even more to consider, however, especially if there is high “noise” or uncertainty connected to statistical hypothesis testing. During validation studies, if a t-test compares the observed default rate (ODR) of a specific rating bucket to its PD, a material difference (e.g., an ODR of 10% versus a PD of 5%) might not be statistically significant if the underlying variance is high. In such cases, further investigation is warranted, despite the test not rejecting the null hypothesis.

Another hypothesis testing scenario involves unexpected test results. For example, the Jeffreys test might indicate underestimation of PD, even if the ODR is 0%. 

Guardrails to Safely Continue Testing

Resistance to null hypothesis significance testing has been fueled by debates over P-values and scientific skepticism. However, it would be unwise and excessive to eliminate all statistical tests for financial risk managers. Rather, the implications of the FWER necessitate establishing guardrails for statistical testing in the field.

The most important guardrail is to require all statistical models to be tested with the help of out of sample (OOS) and out of time (OOT) tests. This means that the model should be applied to a test set that contains data that is entirely separate from the development set. (For OOS, this requires a different sample across the sampling horizon; for OOT, this requires the omission of the most recent cohort of the horizon from the development set.)  This guardrail will allow a risk manager to evaluate the performance of statistical hypothesis testing, particularly with respect to how it measures up to the development set.

Supervisors are emphasizing the need for firms to adopt guardrails against failing statistical procedures in their modeling prescriptions. A recent example is the ECB’s supervisory handbook on the validation of rating systems. The ECB’s updated guide to internal models (2024), moreover, mentions the use of OOS and OOT testing explicitly.

Backtesting is another example of OOT testing. This refers to the cross-validation of the predictive model with the help of historical data, so that the accuracy of the dependencies (as assumed by the model) is continuously tested.

A series of procedures, including backtests, are part of ongoing model monitoring (OMM), which is executed by both the bank and its supervisors. Once a model is in production, it needs to be closely monitored, so that ongoing compliance with regulatory requirements for internal models is verified.

Modelers also need to be continuously trained in sound statistical procedures. They should know that the P-value cannot be used to indicate the strength of a relationship; it is only a statistic to be assessed against a set threshold, as derived from the confidence level.

Other Factors: Reproducibility, Power and Overfitting

Statistical tests tend to have problems with reproducibility. Therefore, samples must be split up into two or even three subsamples, so that the robustness of the driver’s selection can be tested for reproducibility.

What’s more, since t-statistics for individual drivers cannot be relied upon, modelers need to assess these drivers in the context of the model as a whole. A significant t-statistic for a driver within a model with very low overall “goodness of fit” is meaningless.

The concept of the power of a statistical test also needs to be clear. If alternatives are available, it is best to look for available tests with the highest power – e.g., non-parametric tests tend to be less powerful than parametric tests. However, in situations in which parametric tests are less applicable, one may be forced to go for the non-parametric test.

Lastly, modelers must be aware of overfitting risks (especially in ML methodologies) – and should participate in model monitoring.

Overall, banks should establish specific ground rules detailing how statistical tests are planned, executed, interpreted and challenged. Implementing such procedures as part of policy development is an excellent starting point.

Parting Thoughts

Quantifying relationships can be valuable for risk management and for risk/reward decision-making. That’s one reason why financial risk managers often gravitate toward modeling solutions.

However, in the early stages of the modeling cycle — when using prototypes or unofficial challenger models — there's a significant risk of drawing premature conclusions from insufficiently robust statistical tests.

It's therefore crucial to recognize the limitations of the statistical hypothesis testing framework.

For IRB models, risks are typically mitigated through out-of-sample and out-of-time testing and monitoring.  But with respect to credit decision models and challenger/prototype models, statistical testing can yield a higher likelihood of being misled by unreliable test results that lack reproducibility.

By integrating rigorous testing protocols and by maintaining a critical awareness of their statistical limitations, financial risk managers can ensure robust and reliable model outcomes. Indeed, when statistical routines are carefully applied, it is not necessary for the FRM community to throw all statistical testing out the window.

Dr. Marco Folpmers (FRM) is a partner for Financial Risk Management at Deloitte the Netherlands.