A loan portfolio with zero defaults over, say, the past 12 months, is generally considered excellent – as long as the return on the portfolio is strong, of course. However, for credit risk professionals, a portfolio with either zero or very few defaults can lead to headaches.
Low-default portfolios, you see, do not provide sufficient information to validate probability of default (PD) estimates. Sometimes, this is a problem that can yield very strange outcomes, even in zero-default cases.
Indeed, if one automatically applies the Jeffreys test for calibration accuracy to a low-default portfolio, there is a possibility that it will get flagged – not because it’s problematic but rather because the test is complex and doesn’t simply assess the PD by only measuring the number of defaults versus the number of loans.
Red Alert
In a case where the number of defaults equals zero (“D = 0”), the Jeffreys test may, in fact, trigger a so-called red outcome (or red flag), which will ultimately require remedial action for a PD model.
Marco Folpmers
How can such a result be generated under this circumstance? Well, suppose that one validates a portfolio for calibration accuracy and applies the Jeffreys test, per the rating grade, for a bucket of loans. The first PD rating bucket is the 0.03% bucket – the current minimum PD allowed under rules adopted by Basel Committee on Banking Supervision. The loans allocated to this bucket are assigned this minimum PD.
In the context of the Jeffreys test, one collects data on the total number of loans and defaults. But let’s also suppose that there are a low number of loans allocated to this particular bucket (say, 6) that do not contain any defaults.
The allocation of these six loans to the lowest PD bucket is not questioned, since the PD is still positive (0.03%) – albeit at the Basel minimum – and since there are zero defaults in the validation sample. However, despite all of these facts, the Jeffreys test still shows a red flag.
Table 1: Outcome of the Jeffreys Test for an Example Portfolio*
| PD bucket | PD of the bucket (estimated PD) | Nr of Loans (N) | Nr of Defaults (D) | Jeffreys P value | Jeffreys P thresholds (R/O/G) | Jeffreys test outcome |
| 1 | 0.03% | 6 | 0 | 4.89% | ≤ 5%, 5%-10%, > 10% | Red |
* Jeffreys test parameters: D = 0, N = 6, a = 0.5, b = 6.5
How, you may ask, is this possible? The Jeffreys test builds a confidence interval for the estimated PD (in our case, 0.03%) that is based on the empirical evidence – i.e., zero defaults out of six loans. The test then assesses how the estimated PD is positioned relative to this interval.
If it is below the lower confidence bound, a red flag is raised. This happens if the Jeffreys probability falls below 5%. What’s more, an orange flag is raised if it the Jeffreys probability is between 5% and 10%.
For all values above 10%, in contrast, there is a green outcome. This indicates that the Jeffreys test is one-sided: it simply tests whether the PD calibration is at the “right level” or too conservative. Consequently, there can be a red outcome only for the suspicion of a PD underestimation.
Jeffreys Priors: The Cause of Skepticism
From a technical point of view, the Jeffreys test works with a beta distribution, which always has two parameters: a and b. These parameters are determined by the number of defaults (D) and the number of loans (N). In our example, N = 6 and D = 0 .
However, this is not the end of the story. The a and b parameters are also loaded with the so-called “Jeffreys priors” for a and b. In both cases, these are set to 0.5. From here, the a and b parameters are calculated as: a = D + 0.5 and b = N - D + 0.5. These parameters define the so-called posterior distribution of the PD, which is a mixture of the priors on the one hand (a = b = 0.5) and the empirical evidence (D and N) on the other.
We can already see that, for low values of D and N, the impact of the Jeffreys priors is relatively high. This is exactly why, in these cases, the Jeffreys test can deliver counterintuitive results. (Take another look, for example, at Table 1.)
The graph below helps explains the potential harmful impact of the Jeffreys priors.
Figure 1: Jeffreys Probability Density Function – Example 1*
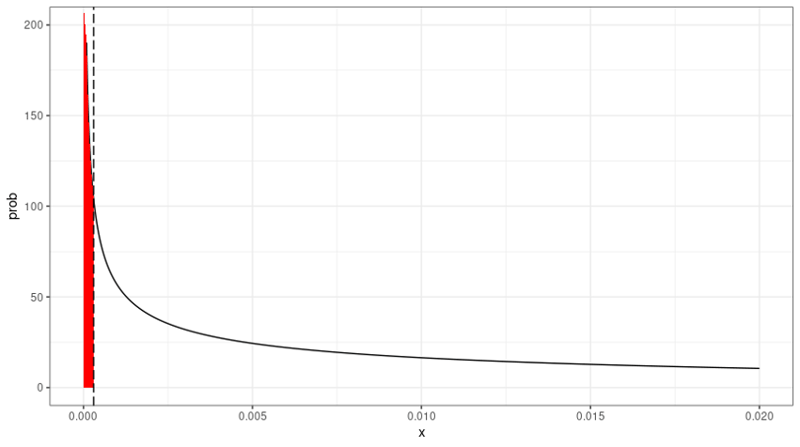
* For N = 6 (number of loans) and D = 0 (number of defaults); estimated PD at 003% (vertical dashed line).
In Figure 1 we see that, with the low number of loans, there’s still much uncertainty about the location of the true (but unknown) population default rate. Given the uncertainty, there’s little probability mass below the 0.03% PD estimate – i.e., the area indicated in red (below the curve, at the left of the 0.03% estimate). If the number of loans would have been 20 instead of six, the graph would have looked like this:
Figure 2: Jeffreys’ Probability Density Function – Example 2*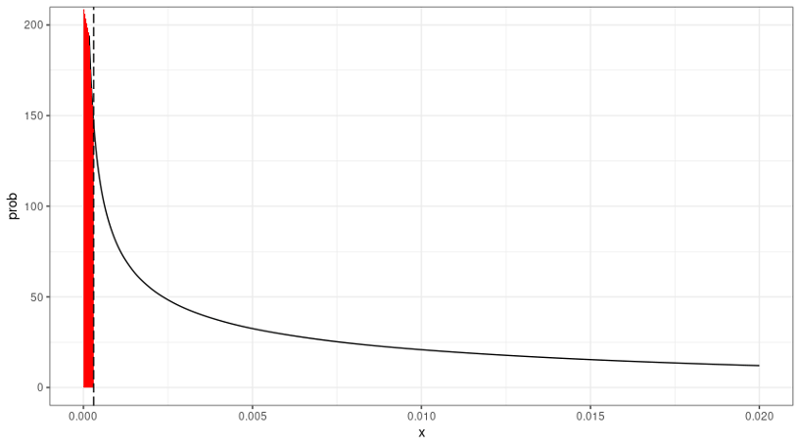
* For N = 20 and D = 0; estimated PD at 003% (vertical dashed line).
For the N = 20 case, we see that the probability density function is less spread out and that there is more probability mass at the low end of the spectrum (indicated, again, in red). In this N = 20 case, the Jeffreys probability has increased to 8.78%, so that it no longer triggers a Red outcome.
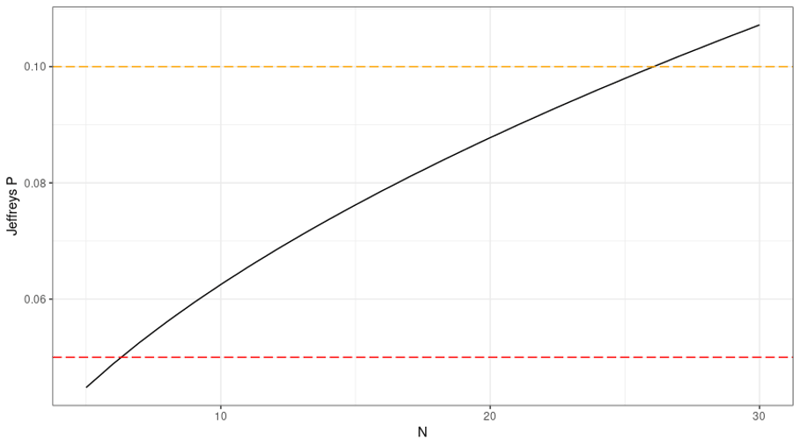
For the zero-default situation (D=0), the two cases illustrated above (for N = 6 and N = 20) are just two special instances of portfolios with zero defaults. The graph below (see Figure 3) illustrates how confidence in the 0.03% PD estimate builds up for an increasing number of observations. We need at least N = 7 to proceed past the red threshold, and at least N = 27 to proceed past the orange threshold.
Figure 3: Jeffreys P for Increasing N (while Defaults = 0)
Parting Thoughts
The problem with the deficiencies triggered by the orange or red outcomes in zero-default cases is that, in the validation process, findings get linked to actions. Consequently, under these scenarios, the PD model will need to be improved, so that any so-called problems can be remediated the next time around, and the finding can be closed.
But what remedial action should one propose for a situation in which the number of defaults is already zero?
There are, I think, two ways to proceed.
The first option is to override the red or orange outcome as an irregularity that resulted from the Jeffreys priors, and to then overrule the outcome to missing or N/A (not available). This is the best way to move forward, particularly if one feels that in the D = 0 cases with low N, the Jeffreys priors have too much impact and lead to a verdict that is too harsh. It is particularly appealing to those risk managers who think a D = 0 case is fundamentally different from other cases (with large N) where red or orange outcomes are triggered.
The second potential solution is to maintain the red (or orange) flag for zero-default cases. Under this approach, a risk manager can adopt a Bayesian framework that comes pre-loaded with Jeffreys priors. In practice, this framework yields a “healthy skepticism” for PD estimation – one that requires more evidence before loans can be allocated to the lowest PD bucket with the 0.03% estimate.
Remedial actions could be difficult to envision, but one could require a PD model to merge the 0.03% rating bucket with the next rating bucket (which could have, e.g., a PD estimate equal to 0.06%). This will lead to a higher PD for affected loans (originally in the PD = 0.03% bucket), and, hence, a greater risk-weighted average RWA.
In most cases, the overall impact of this hybrid approach on RWA will be insignificant, since we are dealing with "D = 0" and “low N” cases by definition. The loans in these grades are typically not the ones that dominate the calculated RWA.
It is difficult to say, ex ante, which proposed solution to the calibration problems presented by the Jeffreys test is more reasonable. In practice, financial risk managers will need to apply professional judgment on a case-by-case basis.
Dr. Marco Folpmers (FRM) is a partner for Financial Risk Management at Deloitte the Netherlands. He wishes to thank Christos Chasiotis, senior consultant at Deloitte Financial Risk Management, for reviewing an earlier draft of this contribution.
Topics: Modeling