Credit Modeling: How to Improve Discriminatory Power

The drive to increase the discriminatory power of a model is like the search for the Holy Grail for credit risk modelers. The quest can be cumbersome, success is not guaranteed, and both endurance and strength are needed to complete the journey.

According to the European Central Bank’s “instructions for reporting validation results,” there are four dimensions for evaluating the performance of probability of default (PD) models: (1) the rating process; (2) calibration; (3) discriminatory power; and (4) stability. Discriminatory power is the most important of these high-level criteria.

Marco Folpmers

For professional credit risk modelers, the first and second activities can be planned and executed. Calibration, for example, is relatively straightforward for the calculation of the long-term default rate. Indeed, the conversion of continuous PD outcomes of the model to the PD master scale can be calibrated in such a way that the portfolio PD is ultimately sufficient, both at the aggregate level and for the individual rating grade.

Improving the discriminatory power, on the other hand, is more cumbersome. Unlike calibration, increasing the power of a model is not within the immediate scope of the modeler.

If a model has insufficient discriminatory power, it is not easy to increase it. In some cases, more modeling efforts can remediate insufficient power – but that is (unfortunately) not always the case.

A 2023 European Banking Authority report on machine learning (ML) showed that banks are now turning to ML approaches to improve the discriminatory power of the internal ratings-based (IRB) models. But this is not necessarily the wisest strategy.

ML models can only make a difference if the modeling dataset is extensive and if the bank has sufficient analysts and brainpower to develop and properly test ML models. Moreover, as the EBA’s report elaborates, for the ML-driven discriminatory power approach to work, the data and routines it uses need to be “traceable.”

Let’s now examine why data is so critical, and then explore the best approaches for improving a model’s discriminatory power.

The Need for More Data

The root cause of insufficient discriminatory power is often the lack of data for risk drivers that allow for the sufficient separation of loans that are more likely to perform in the future versus those that are more likely to default.

If the available risk drivers are insufficient, even applying the most advanced ML routines will not improve the model performance. Indeed, the switch to ML models is only beneficial if the modeler has a large dataset – e.g., tens or, preferably, hundreds of variables – from which to choose. More data is often acquired by pulling in more client data (sometimes acquired from outside suppliers) or transactional data (payment data).

Of course, there is no guarantee about whether the acquisition of more data will ultimately lead to a better model. Given this uncertainty, one wonders if there are other and more focused steps a firm can take to improve discriminatory power.

ROC and AUC

When attempting to improve discriminatory power, it is important to incorporate specific risk drivers. We can start by enhancing the receiver operating characteristic (ROC) curve and the area under the curve (AUC).

Below, we show the ROC curve for a credit risk modeler who is assessing the discriminatory power for a PD model fitted to an example small and medium-sized (SME) portfolio of 1,000 loans, with a calibrated PD of 1.5%.

Figure 1: A Typical ROC Curve

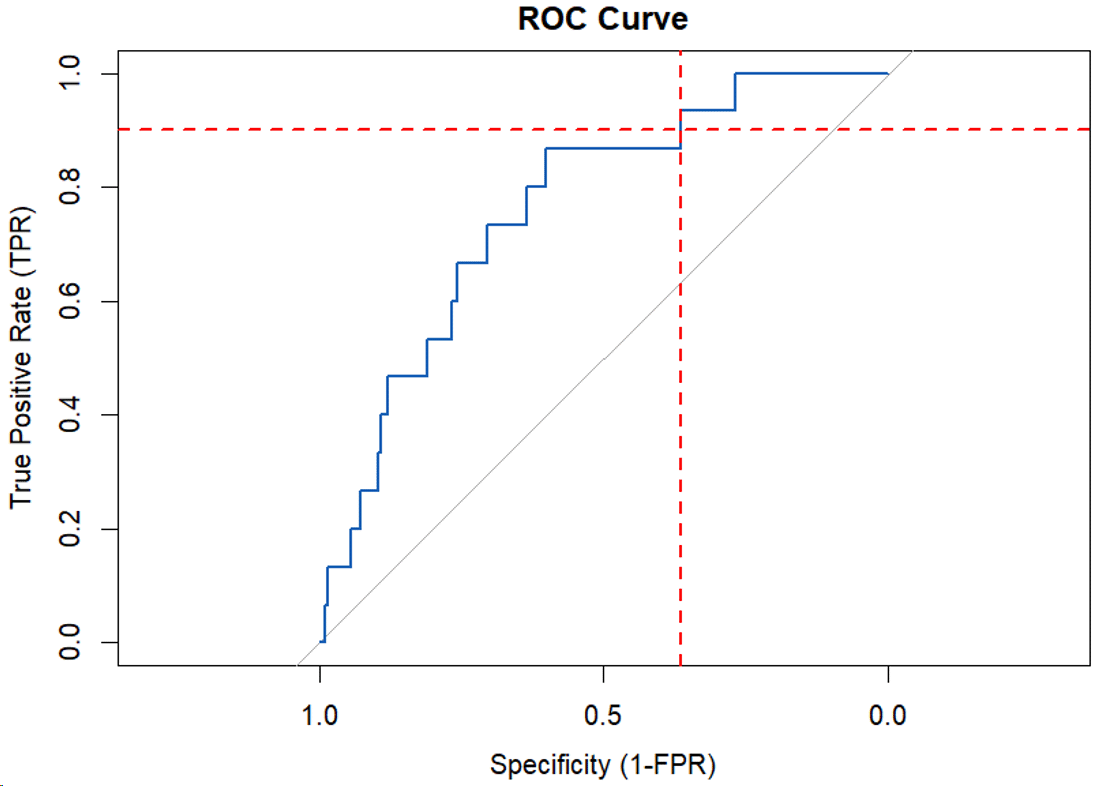
The discriminatory power can be expressed as the AUC. In Figure 1, this is the area under the blue curve. The higher the AUC, the better. (The grey line in Figure 1, with the 45-degree angle, shows a random model that has an AUC of 50%.)

Before figuring out how to increase the discriminatory power of the model depicted in the figure above, we must first study it closely. The underlying situation is that all loans depicted in Figure 1 received a continuous risk score. Based on this score, one can allocate loans to a default prediction or to a performing prediction.

One is free to choose the cutoff point above which one will allocate a loan to a default prediction. If one uses a high cutoff point, the risk indicator value must be quite high before this rule will allocate a loan to a default prediction. In such cases, one is more likely to fail to allocate a bad loan to a default prediction than to erroneously allocate a good loan to a default prediction.

Conversely, if one uses a low cutoff point, the opposite will be true – i.e., we’ll see more erroneous default predictions for good loans.

When aligning a credit risk situation with the ROC terminology, it’s important to remember that “positive” refers to a default indicator that is positive. (This is a recurring cause of confusion, since a default is not a “positive” experience for the bank, let alone the client.)

TPR vs. FPR: Sensitivity and Specificity

On the y-axis of Figure 1, one sees the True Positive Rate (TPR) – or the ratio of predicted positive loans out of all positives. As shown in Table 1 below, this is also called the sensitivity (TPR = sensitivity = TP/P).

The x-axis of Figure 1 shows specificity – i.e., 1 minus the False Positive Rate (FPR). The FPR (which complements specificity) is the ratio of false positives out of all negatives (FPR = FP/N). It can be used to help calculate specificity, which is the ratio of true negatives out of all negatives (specificity = TN/N = 1 - FPR).

Table 1: Understanding TPR and FPR

When modeling for classification, there is a trade-off between sensitivity and specificity. If one wants a 100% sensitivity, the model will predict that all loans will go into default, with the help of a very low threshold (TPR = TP / P will be 100%). However, under that scenario, the specificity will be very low, because there will also be a lot of false positives (FP/N is high, specificity is low).

A model with a high discriminatory power will make it possible to better balance between sensitivity and specificity. The model shown in Figure 1 is less than ideal, with an AUC of 76%.

In credit risk, it is more serious to fail to predict a default than to erroneously flag a performing loan as a predicted default. This means that sensitivity for positive default identification is more important than specificity.

Suppose that we require our model to have a sensitivity of at least 90%. As we can see in Figure 1, the maximum attainable specificity (see the dotted red horizontal and vertical lines) is then 36%.

The TPR/FPR matrix for this targeted sensitivity/specificity combination is depicted in Table 2. Note that P/(P+N) equals 1.5%, which is our calibrated PD level.

Table 2: Understanding TPR and FPR for a Sample Portfolio

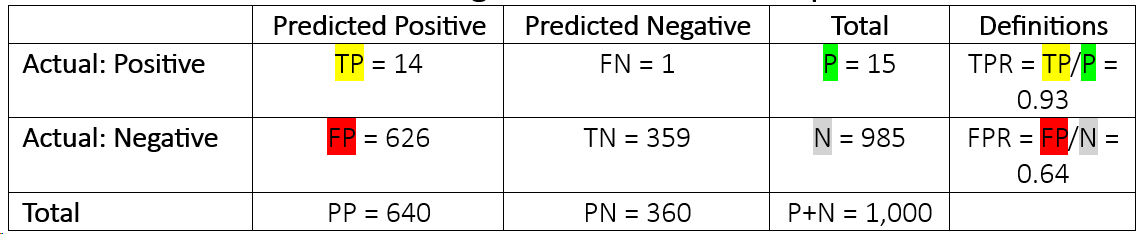
A specificity of 36% is not that high; it means that out of all good loans (shown as negative, or “N,” on the default indicator), 64% are erroneously flagged as predicted default (FPR = 1 – specificity; FPR = FP/N). So, under this scenario, more than half of the performing loans are erroneously predicted to default within one year.

By requiring the TPR to be above the stated target level of 90% (because we don’t want to miss too many future defaults), it is necessary to increase the number of false positives (FP), given the current power of the model.

The challenge credit risk modelers face is how to increase TP to the desired target level without simultaneously increasing FP.

Searchlight vs. Lighthouse

One traditional approach is a “lighthouse” technique that attempts to improve model power through a broad sweep of data that essentially shines light in all possible directions. But we may be able to find a better solution to the discriminatory power dilemma through a so-called searchlight approach that more closely scrutinizes TP and FP loans.

The idea is to sample, say, 12 files from the TP group and 12 from the FP group – and to then inspect these loans with the help of a diverse group of professionals that includes modelers, relationship managers and the financial restructuring and recovery unit (FR&R).

When evaluating these files, the following questions should be asked:

1. Why have all 24 loans been predicted as positive on the default indicator? How similar is this group, moreover, given the properties of the current model? (This first step is to verify that the model has been applied properly and the modeling logic is understood.)
2. In what respect are these two groups of loans different? For this step, it is crucial to hear the stories from FR&R. What circumstances or drivers, for example, have led to the actual defaults in the TP group?
3. Finally, what specific data drivers are pertinent for this TP group?

This inspection can help characterize more specifically the TP group, while at the same time leaving out the loans of the second (FP) group. Using this searchlight approach, we can see, for instance, that SME loans in our example portfolio have migrated to default status, because of corona support repayment obligations.

By adding a more specific risk driver for the corona support repayment obligation, the searchlight approach leads to improved discriminatory power, which may, in turn, help a modeler attain a better specificity for the same sensitivity. If this driver is not in the model dataset, the threshold of the risk indicator (based on the current drivers) needs to be very low to reach the target sensitivity value of 90%.

The traditional data-driven lighthouse approach, on the other hand, casts a an extremely broad net, which typically means that a lot of good loans are erroneously flagged as future defaults.

So, which approach is better? The table below compares and contrasts the lighthouse and searchlight approaches to the discriminatory power challenge.

Table 3: Lighthouse versus Searchlight

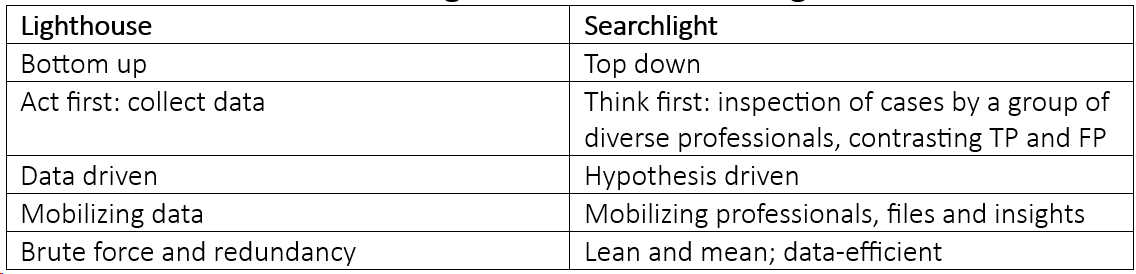
While a significant expansion of the available data for modeling (i.e., the lighthouse approach) is often the first solution to the low-model power problem, it is not the best.

The searchlight technique is a more specific and hypothesis-driven way to detect specific risk drivers and is considered by some practitioners as more elegant than the traditional data-driven, brute force lighthouse approach.

Parting Thoughts

Discriminatory power is the most important of the four elements of model performance – but it is also the most difficult to attain. If a model has been improved after many iterations, it is difficult to understand how one can generate additional explanatory power.

Linking significantly more data, and then applying advanced techniques to create powerful new risk drivers, is one solution for this dilemma. Known as the lighthouse approach, this solution can be successful when it efficiently combines big data with ML models.

However, top-down searchlight solutions can often work equally well – and are sometimes even superior – because they start with a better understanding of the ROC curve and rely on a diverse group of professionals within the bank to compare TP and FP group predictions.

Through the searchlight approach, one can mobilize specific data for increased model power, instead of relying exclusively on big data and ML.

Dr. Marco Folpmers (FRM) is a partner for Financial Risk Management at Deloitte the Netherlands.