Last month, the European Banking Authority (EBA) issued a new report that sounded the alarm about increasing geopolitical tensions and geoeconomic fragmentation. In response, banks have taken steps to improve their resilience, partly through using advanced tools (like stochastic matrices) that can monitor and measure evolving geopolitical trends.
Geopolitical risk, says the EBA, can be divided into several different categories – such as cyberattacks and the enactment of tariffs and sanctions. These threats are affecting both bank performance and financial stability through so-called “transmission channels” – including, for example, the “real economy.”
Banks therefore need robust techniques to analyze how geopolitical threats are impacting both their risk profile and their clients. Let’s now consider what this entails and what tools and techniques banks can use to monitor, assess and mitigate wide-ranging geopolitical risk.
Risk Buckets and Classification: A Great Place to Start
Dr. Marco Folpmers
Specific drivers of geopolitical unrest can be translated into discrete buckets. How dependent, for example, is a client on revenues from exports – or from the import of scarce raw materials for which future price increases and shortages are expected? The underlying idea is that unrest, as an abstract concept, can be measured and monitored in a concrete way.
Breaking down exposures by risk buckets, and tracking their movements, is an important component of financial risk management. Probability of default (PD) and loss given default (LGD) are two of the more well-known risk buckets.
These risk buckets (which collectively contain all exposures) can be ranked into ordinal classes, from low risk to high risk. Classification exists in discrete time – e.g., exposures can be in a high-risk bucket at one time and in a low-risk bucket at a later date, or vice versa. Each individual exposure can be measured across different periods of time (throughout its lifetime), and as it moves across buckets.
In addition to the risk parameters PD and LGD, we can also think of risk buckets that address underlying causes more directly. We can, for example, classify a loan by length of time it is in arrears – e.g., “no arrears,” “less than 2 weeks,” “between two weeks and one month,” “between one month and 90 days,” and “more than 90 days.”
Risk driver information is also crucial. An example is the debt service coverage ratio (DSCR), which can be classified as staying roughly the same, worsening or improving. Alarm bells should ring at credit risk management units when there is heightened inflow in the worsening DSCR bucket.
The Transition Matrix
The most important tool for the analysis of the risk buckets is the transition matrix – also known as the “stochastic matrix.” These matrices are typically estimated with the help of historical data of stage transitions (e.g., monthly snapshots) in discrete time.
An example of a transition matrix is provided in Figure 1 (below). The percentages refer to probabilities to move from one DSCR bucket (1 = very good; 5 = very bad) to another at the next point in discrete time (say, after a month). For example, at row one, column five, a percentage of 0.50% is listed. This means that there is a 0.50% probability that an exposure that is currently in bucket 1 will be in bucket 5 the next month. This is an example of a severe deterioration of the quality of the exposure.
Figure 1: A Migration Matrix for a Debt Service Coverage Ratio
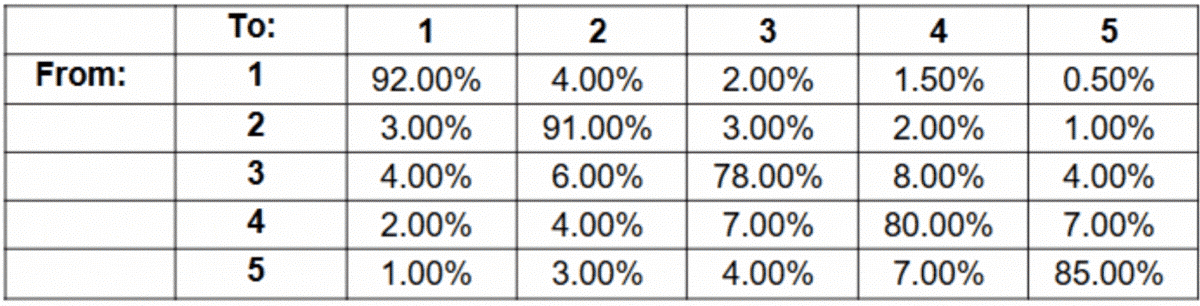
Migration matrices should be checked, so that all rows sum to 100 percent. Indeed, this is a technical requirement that is conditional to all further analysis.
Large percentages across the main diagonal of the matrix – running from (1, 1) to (5, 5) – are expected. The further we are removed from the main diagonal, the smaller the expected percentages. All movements to the right and above the main diagonal are deteriorations of the risk, whereas movements to the left and below this diagonal are improvements.
Derivation of the Steady State
From a starting distribution across risk buckets at time t = 0, one can easily derive the distribution for t = 1 by multiplying the vector of the starting distribution with the transition matrix. We can from there the derive the distribution for t = 2, et cetera.
By repeating this multiplication often enough, one finally converges toward the so-called steady state distribution. In this state, the multiplication with the transition matrix does not change (materially) the resulting distribution.
This is quite important, because it informs us about where the transition matrix is ultimately going. If we see that the underlying dynamics will lead to, say, all exposures ending up in the two worst DSCR buckets, red flags should be raised.
The impact of repeated multiplication can be seen in Figure 2 (below), which starts with an equal distribution across the five buckets.
Figure 2: Convergence to Steady State
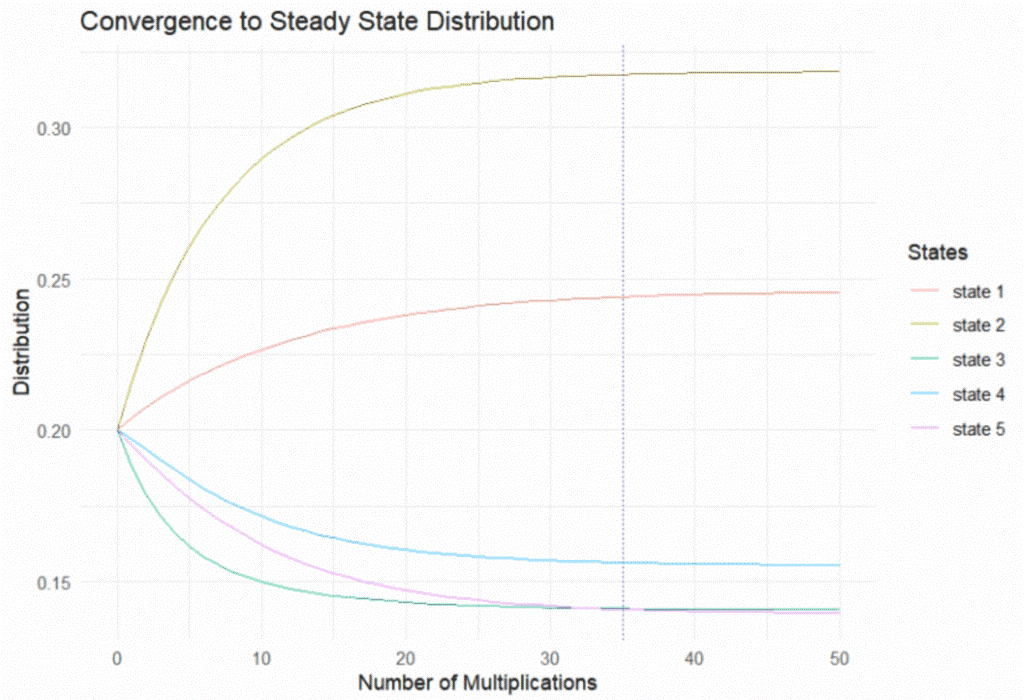
In our example, we see that the steady state will lead to exposures that are predominantly distributed across states 1 and 2. We also see that a large number of multiplications is needed before convergence is attained. State 5 (the pink line) initially has a higher share than state 3 (the green line), but the situation is reversed in the end, with the green line sitting above the pink line. The cross-over point is at 35 multiplications.
To avoid wrong conclusions, the convergence criteria need to be established diligently.
Going Straight
Luckily, there are ways to derive the steady state immediately. We can achieve this by decomposing the transition matrix into its eigenvalues and eigenvectors. Providing a full explanation of eigenvalues and eigenvectors is beyond the scope of this article; for our purposes, it’s sufficient to say that they are very useful.
In an [n, n] matrix, the transition matrix is a special case. There are n eigenvalues and n eigenvectors, each of size [n, 1] – and one specific eigenvalue relates to one specific eigenvector. The transition matrix has one eigenvalue equal to 1, and the steady state is equal to the standardized eigenvector that corresponds to this eigenvalue. In our example, the analytical steady state vector is therefore {0.2460, 0.3186, 0.1406, 0.1553, 0.1394}.
The advantage of this analytically derived steady state (Figure 2) is that one need not bother with convergence criteria, which runs the risk that not enough multiplications have been performed.
The steady state vector also gives immediate insight into the question about whether there are absorbing states – i.e., a state that always retains an exposure after it is received. If there is only one absorbing state, all exposures will end up in that state. If there are multiple absorbing states, the exposures will end up in one of them, depending on the starting distribution. In our example, it is clear that there is no absorbing state.
The routines to derive the eigenvalues and eigenvectors can be easily implemented with the help of analytical software environments that support discrete mathematics. One caveat is that some banks use very advanced techniques in which the migration matrix itself changes over time. In such cases (where a steady state may even not exist), it is no longer possible to go straight to the steady state with the help of eigenvalues/eigenvectors; rather, one must work through the multiplications for the projections.
Parting Thoughts
Financial risk managers (FRMs) need strong analytical tools in times of heightened geopolitical risk. These tools can track exposures across time and across different risk buckets – not only for PD and LGD but for underlying drivers of risk, like DSCR.
A careful analysis of risk buckets and their underlying drivers can show the direct impact of geopolitical risk on the “real economy,” as well as on a bank’s risk profile and on the financial health of a bank’s clients. If a bank detects, for example, that its risk appetite limits will be broken soon, it can issue an early warning.
What’s more, with the help of transition matrices, banks can more accurately project the future distribution of individual risk exposures across different risk buckets. Overall, in times of heightened geopolitical volatility, it is very useful for banks and their FRMs to add analytical tools and discrete mathematics to their toolset.
Dr. Marco Folpmers (FRM) is a partner for Financial Risk Management at Deloitte the Netherlands.
Topics: Modeling