
Economic capital has always been a key measure of a bank’s solvency. But under Basel III, the set of international banking regulations that are scheduled for implementation next January, proper calculation of economic capital will become even more vital.
Basel III will not only limit the use for the most advanced (AIRB) models for low-default portfolios but will also feature an output floor that will require risk-weighted assets (RWA) resulting from internal models to be no less than 72.5% of the standardized RWA. In short, under this accord, regulatory capital will become less risk sensitive. Economic capital will consequently be elevated to a new level of importance – particularly with respect to a bank’s risk/reward steering.
As a measure of a bank’s ability to survive all of its risks, economic capital distinguishes itself from RWA in that it can better manage correlation and diversification within the portfolio. To fully reflect concentration and diversification in the portfolio, the economic capital amount must first be calculated at group level. For risk/reward steering, it subsequently needs to be allocated to the individual business units (BUs).
Before we take a closer look at the benefits of the covariance allocation approach, let’s first examine an example portfolio for economic capital calculation.
Example Portfolio
The allocation of the group economic capital to the BUs can be illustrated with the help of a simple example. Consider, for instance, a small portfolio of 200 loans that have been originated by four BUs.
Let’s say that these loans have an average probability of default (PD) of 4.43%, a loss given default (LGD) that is fixed at 40% and an exposure at defaults (EAD) equal to €100,000. The expected loss of €354,400 can be calculated, simply, as follows: 4.43% * 40% * €100,000 * 200.
Consider also that the loans (originated by the 4 BUs) have been extended to a corporate portfolio that distinguishes between seven possible industries. BUs 1, 2 and 3 have a portfolio of loans that are dispersed across industries 1 through 5, while BU 4 has loans only in industries 6 and 7. Obviously, BU 4 is less diversified than the other BUs.
This example is illustrated in the Figure below, where we see that BUs 1, 2 and 3 have a portfolio of loans that are dispersed across sectors 1 through 5, while BU 4 only has loans in the industries 6 and 7.
Figure 1: Business Units and Their Investments Across Industries
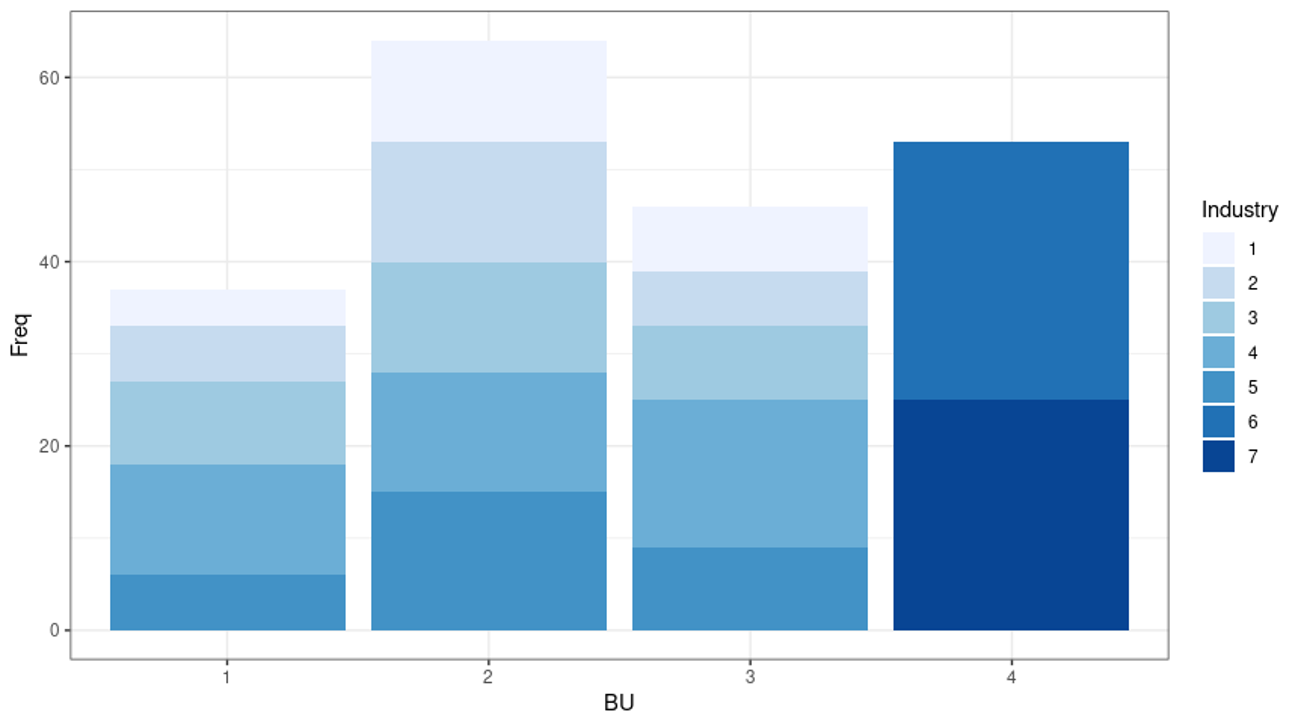
It is important to point out that, in contrast to BU 4, BUs 1, 2 and 3 do not invest in industries 6 and 7. This distinguishing feature will prove to be a decisive element in the allocation of group economic capital to all of the BUs.
Supply-Chain Correlation
Firms that deliver goods and services to each other within the supply chain represent industries in our example. The health of these industries is correlated with the financial health of adjacent industries (their supplier and clients), but not so much further upstream or downstream.
Figure 2 (below) depicts the correlation matrix for the indicators of financial health of the seven industries in our example. Matrices like these are typically based on return statistics for the equity indices of these seven industries.
Figure 2: Industry Correlations
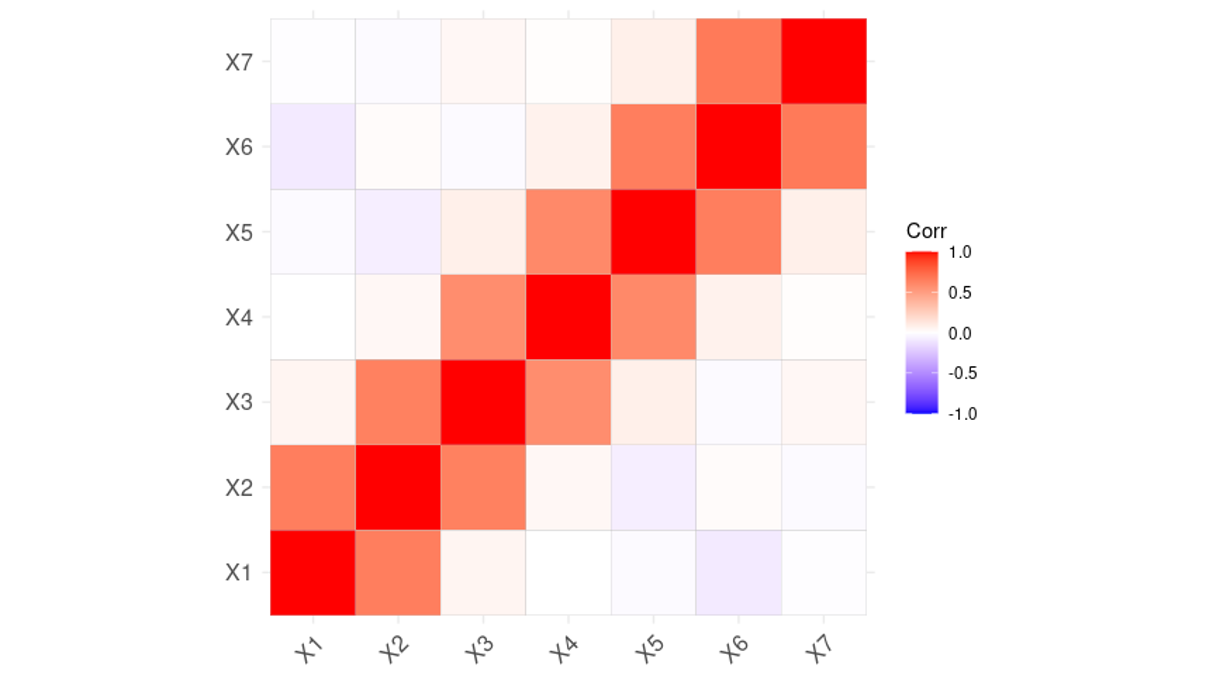
So, let’s look again at BU 4. It is less diversified than the others, because it is only invested in two industries (instead of five) and because those industries are closely related via a supplier/client relationship. The financial health of the two BU 4 industries is therefore highly correlated.
Group Quantification and Scenario Analysis
For the quantification of group economic capital, a multi-scenario simulation must be set up. In each scenario, a credit-risk loss, at the group level, must be determined.
The “financial health” of each scenario can be determined using an individual obligor/loan that considers both an idiosyncratic factor (circumstances specific to the obligor) and a systematic factor. The systematic factor is based on the financial health of the industry (one of the seven aforementioned industries) of the obligor.
Considering all of these factors, we can use the following equation to calculate the economic capital for the group:
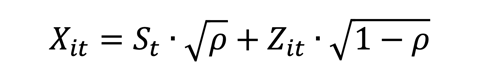
In this formula, Xit is the financial health of obligor i in scenario t. This financial health is dependent on the idiosyncratic factor Z and the systematic factor S. As said, this systematic factor S is usually the industry to which obligor i belongs. Often, S and Z are sampled from standard normal distributions.
In our example, there’s a high degree of systematic risk (in line with that of a corporate portfolio), and ρ is set at 0.7. An obligor is expected to go into default as frequently as predicted by its PD. This is implemented, per scenario, by switching an obligor to a default state as soon as Xit is below the normal inverse of the PD (the threshold equals N-1 (PDi )).
After simulating many economic capital scenarios, the statistical loss curve (see Figure 3) is derived where the economic capital is quantified as €2.2 million – the difference between the 99th percentile and the expected loss of €354,400, as stated above.
Figure 3: Statistical Loss Curve
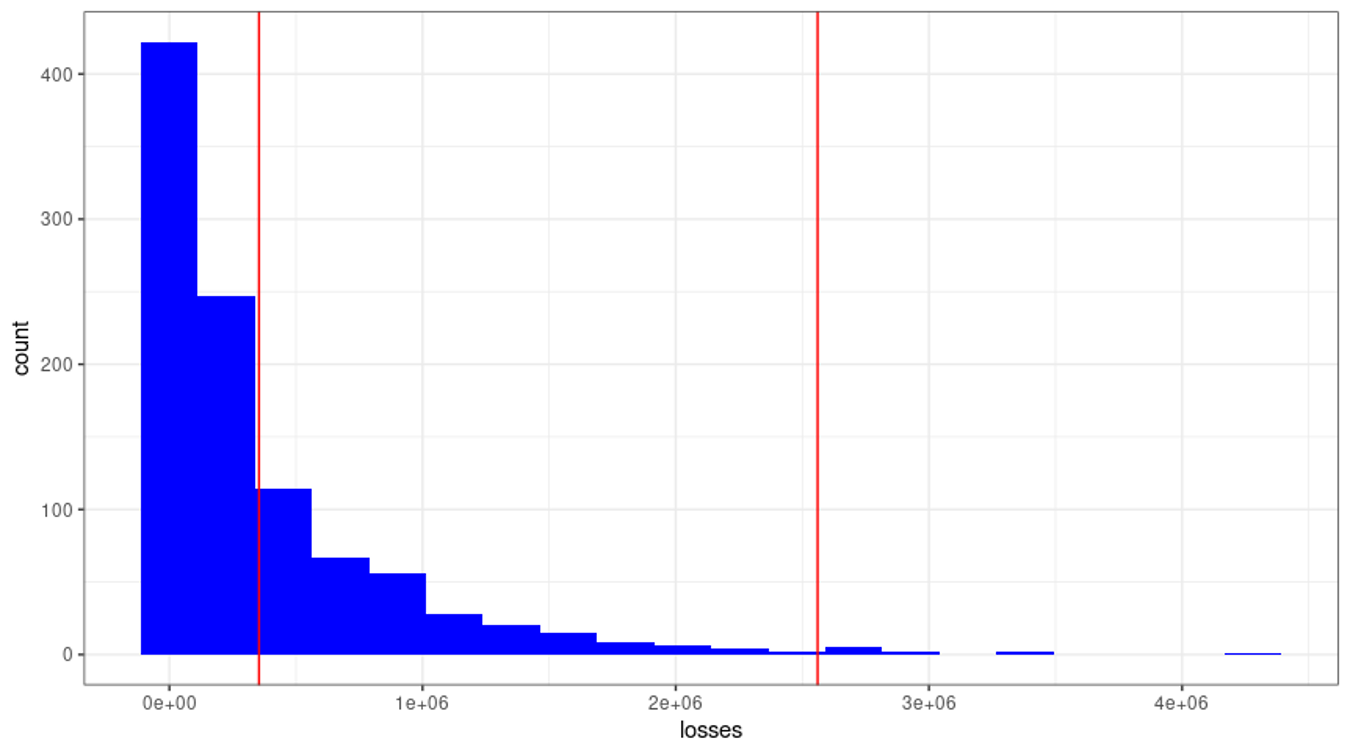
In Figure 3, the economic capital is the distance between the two red vertical lines. This shape of the statistical loss curve is typical of a portfolio with a high systematic risk (ρ). For lower levels of systematic risk, the curve resembles more the shape of a lognormal distribution.
Allocating EC to Business Units
One of the most intriguing questions around economic capital is how to allocate the economic capital to the BUs.
The challenge with economic capital is that it originates at the portfolio level. Since economic capital calculation takes all concentrations and diversifications within the group into account, EC must be allocated to the individuals BUs – for instance, for risk/reward steering.
Several options have been proposed for this task. One is to allocate economic capital on a standalone basis. Under this approach, economic capital is calculated separately for each BU, and the resulting numbers are used for allocation.
The problem is that this type of standalone allocation does not take into account that BU 4 is fundamentally different from the other BUs. From a performance management point of view, neglecting this difference is a weakness, since one wants to incentivize BUs to explore diverse business opportunities that align well with the business of the rest of the bank.
Another possibility is to use component VaR. Under this approach, one calculates economic capital for all BUs, both with and without each specific BU. (For example, with and without BU 1.) The difference between the two amounts (with/without) is the amount that a specific BU (1, 2, 3 or 4) adds to group EC.
The disadvantage is that these component VaRs do not necessarily sum up to group EC, and therefore need to be scaled. However, as opposed to allocation based on standalone economic capital, the component VaR method uses comprehensive portfolio data to allocate economic capital to specific BUs.
Benefits of Covariance Allocation
Fortunately, there is a much better economic capital allocation method for BUs: the covariance allocation principle. According to this principle, each BU gets a share allocated of group economic capital (where b is the index for the BUs), as follows:
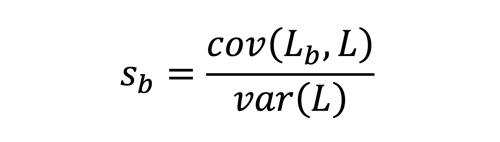
In this formula, var (L) is the variance of the group losses of all scenarios. These are the same group losses that were depicted on the statistical loss curve of Figure 3.
Lb is the vector of losses of BU b. Since the vector L is the sum of the vectors of BUs’ losses, the sum of the covariances (between the BU losses and group losses) is equal to the variance of the group losses. It then follows that the weights sb sum to 1, as they should according to the full allocation principle.
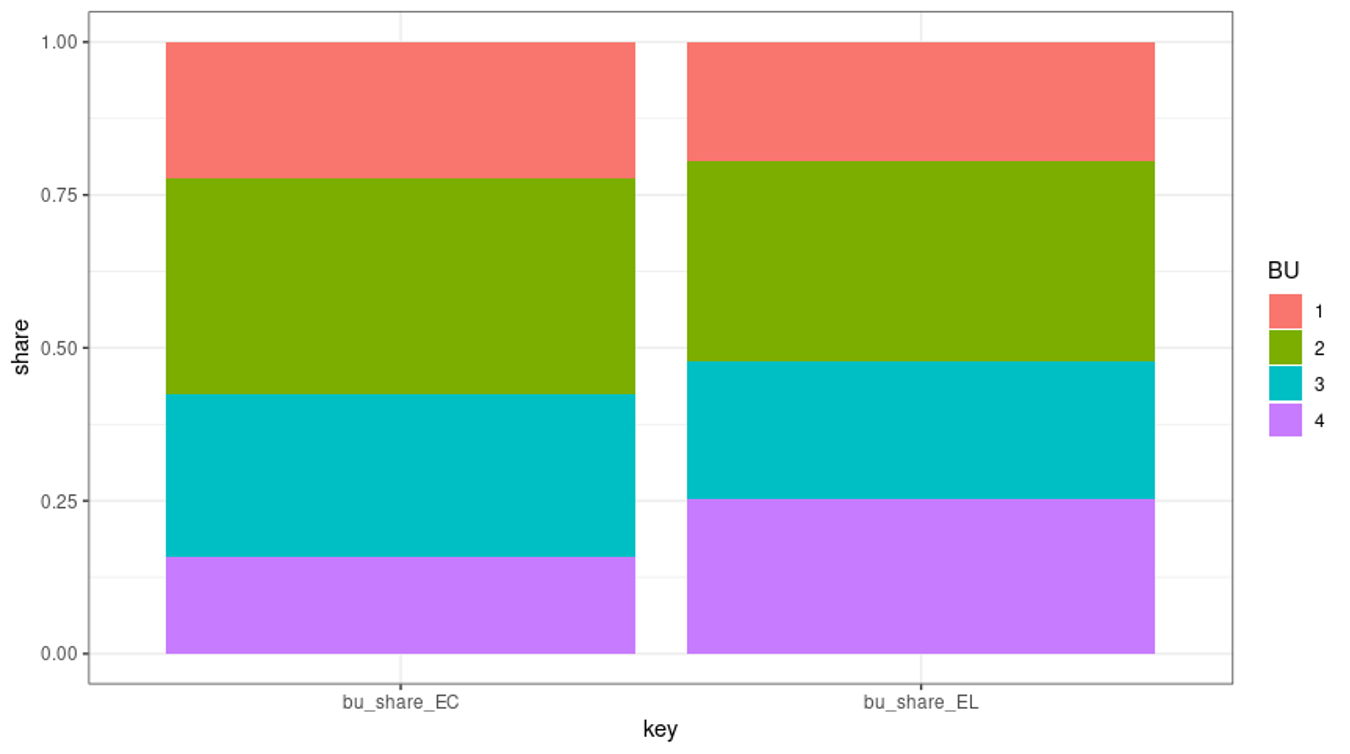
The covariance allocation principle also uses full information: if the losses of a specific BU have a low correlation with the group losses, it diversifies the portfolio, and that BU receives a smaller share of group economic capital (ceteris paribus). As illustrated in Figure 4 (below), using this approach, the allocation of the group economic capital to BU 4 is less than what one would expect on the basis of expected loss.
Figure 4: Allocated Economic Capital vs. Allocated Expected Loss
The inner-workings of the covariance allocation principle are driven mainly by the correlation matrix for the business losses and the group losses, as depicted in Figure 5.
Figure 5: Loss Correlations
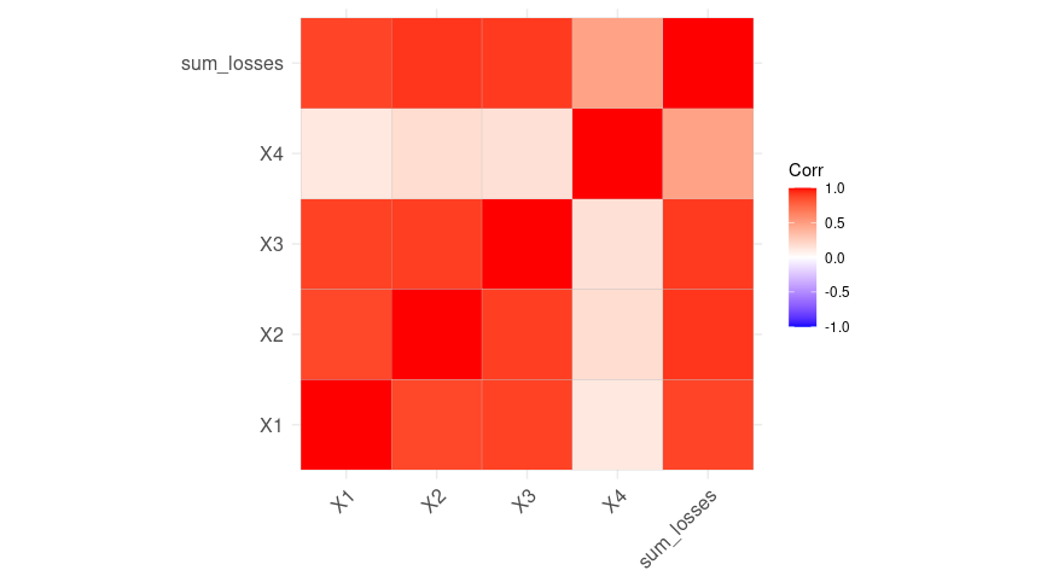
As illustrated in Figure 5, it is clear that BU 4 has a highly specific profile: it correlates less with the other business units; moreover, its correlation toward the sum of the losses is significantly lower.
Parting Thoughts
As the implementation date for Basel III draws nearer, the importance of proper economic capital calculation has risen. Economic capital does a better job of capturing risk/reward information than regulatory capital, and EC will therefore be vital for risk/reward steering in a regulatory environment with less RWA risk sensitivity.
While there are multiple options available for allocation of group economic capital to BUs, one stands out, for both its simplicity and its elegance: the covariance allocation principle.
Dr. Marco Folpmers (FRM) is a partner for Financial Risk Management at Deloitte Netherlands.
Topics: Modeling